*folds world map in half
*sticks pencil through
this post was submitted on 20 Aug 2024
438 points (97.6% liked)
Memes
51523 readers
1614 users here now
Rules:
- Be civil and nice.
- Try not to excessively repost, as a rule of thumb, wait at least 2 months to do it if you have to.
founded 6 years ago
MODERATORS
I honestly believe that sometimes, my genius, it generates gravity.
You youngsters with your Einstein Rosen-bridges! Always in too much of a hurry to take the scenic route!
load more comments
(2 replies)
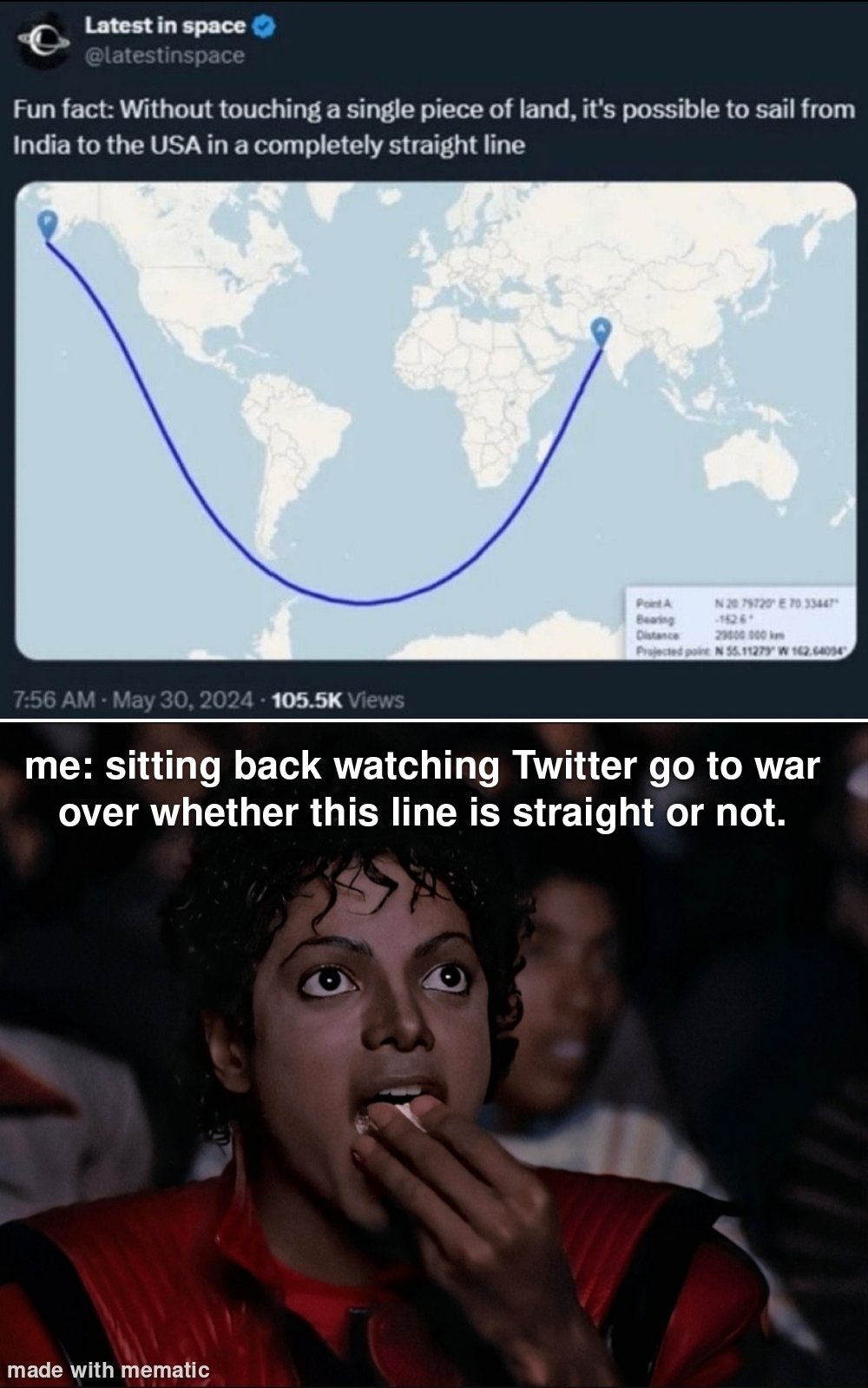
Low IQ: it's not a straight line
Medium IQ: it's a geodesic on a sphere, so it is a straight line
High IQ: it's not a straight line
He's right, you know.
About the line?
About everything, damn it!
It's a straight line through non-euclidean space
unfortunately in reality it is a curved line on a sphere
In actual reality there would be wind and water currents diverting any ship sailing that route from the depicted "line" anyway so the whole argument is pointless
The only straight line paths in the universe are followed by electrostatically uncharged non-accelerating objects in free fall in a vacuum. Or massless particles.
What if we assume the ship is actually a spherical cow
load more comments
(3 replies)
It can get a few percent longer if sailing between Madagascar and the rest of Africa but Pakistan-Russia does not have the same ring to it, I guess.
Edit: source (German), they also show the longest land route (across Eurasia of course)
load more comments
(8 replies)
Today on the internet: Fun with spherical geometry.
This reminds me of some maps by Andy Woodruff.
They weren't made to find long lines, and picking out a single line can be a tad difficult, but it's very interesting nonetheless.
Well there's the one guy in Northern India who gets a peek at South America from between Madagascar and the African continent.
load more comments
(1 replies)
Space-time itself is curved, therefore there is no such thing as a straight line.
Not true, as when space bends, it bends the rulers and compasses too. We experience no spatial distortion.
A person traveling near the speed of light doesn't feel like time is slower for them (but it is and we can measure it)
The principle is equivalent.
That said, it's not a straight line in any topology standard I am aware of.
Sure you could CREATE a topology framework where this would be considered a straight line, but there is no real world model that could come even close without so much mass being concentrated in static relative areas, and EVEN THEN it would only be straight for a predetermined instant before the mass deforming spacetime began interacting with each other.
That's the problem with spacetime deformations, almost no layman takes into account the ridiculous amounts of static mass to make those strange topologies.
Space-time itself is curved, therefore everything is moving in a straight line, it only appears to be curved to the outside observer
load more comments
(6 replies)
Every line is a straight line in one dimension
Your dad and I think you should start looking for a job.
I can't legally work in my country I'm not old enough
Globists will argue that on a globe this is a straight line. Seen these arguments before, don't work on me
Nice. Be proud.
Dunno what of, but be proud anyway!
Thanks! I'm very proud of seeing the truth. Watch this short video and you will being to understand. But watch it to the end, it's short enough
The ending really brings the whole video together. Thanks for sharing!
load more comments
(1 replies)
How can any line that is on the surface of a sphere be straight rather than a curve?
it's a bit of a "spirit of the law vs letter of the law" kind of thing.
technically speaking, you can't have a straight line on a sphere. but, a very important property of straight lines is that they serve as the shortest paths between two points. (i.e., the shortest path between A and B is given by the line from A to B.) while it doesn't make sense to talk about "straight lines" on a sphere, it does make sense to talk about "shortest paths" on a sphere, and that's the "spirit of the law" approach.
the "shortest paths" are called geodesics, and on the sphere, these correspond to the largest circles that can be drawn on the surface of the sphere. (e.g., the equator is a geodesic.)
i'm not really sure if the line in question is a geodesic, though
You are absolutely correct, but to add on to that even more:
When we talk about space, we usually think about 3D euclidean space. That means that straight lines are the shortest way between two points, parallel lines stay the same distance forever, and a whole bunch of other nice features.
Another way of thinking about objects like the earth is to think of them as 2D spherical manifolds. That means we concern ourself only to the surface of the earth, with no concept of going below the surface or flying up into the sky. In S2 (that's what you call a 2D spherical manifold), and in spherical geometry in general, parallel straight lines will eventually cross, and further on loop back and form a closed loop. Sounds weird, right? Well, we do it all the time. Look at lines of Longitude, for example.
We call the shortest line connecting two points in curved manifolds geodesics, as you said, and for all intents and purposes, they are straight. Remember, there is no concept of leaving the sphere, these two coordinates is all there is.
What one can do, if one wants to, is embed any manifold into a higher-dimensional euclidean one. Geodesics in the embedded manifold are usually not straight in higher-dimensional euclidean space. Geodesics on a sphere, for example, look like great circles in 3D.
load more comments
(1 replies)
load more comments
(6 replies)
By defining the coordinate system as a sphere.
Basically, there are multiple right answers, but the most correct answer depends on how you define coordinates.
In “simple”, xyz it’s not a line.
In Euclidean geometry, a straight line can follow a curved surface.
In bullshit physics, everything is warped relative to spacetime so anything can or cannot be a line, but we won’t know.
load more comments
(1 replies)
THAT would be one god damn brutal sail. Both horns, Southern Atlantic crossing followed up by the Indian Ocean.
The range of foulies you would need to bring would be 3/4 of your pack. Foulies underwear and A sock (you're going to lose one anyways)
load more comments
(4 replies)
Would clarifying words have helped? "If you only sailed with forward force..." or "Following along the surface of the earth..." or... what?
Obviously they mean that you don't need to make any turns and that straight means an arc around the earth and not through the Earth, unless someone has a very different idea what sailing means...
load more comments
(2 replies)
Why'd they go that way? They could have gone the other way and the line would have still been technically straight, but the route looks like it would have been shorter.
Because going in that route would make it touch land which in the twitter post it says straight line without touching land
load more comments
(5 replies)
load more comments
(4 replies)
view more: next ›