this post was submitted on 27 May 2024
973 points (100.0% liked)
196
16589 readers
1931 users here now
Be sure to follow the rule before you head out.
Rule: You must post before you leave.
founded 1 year ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
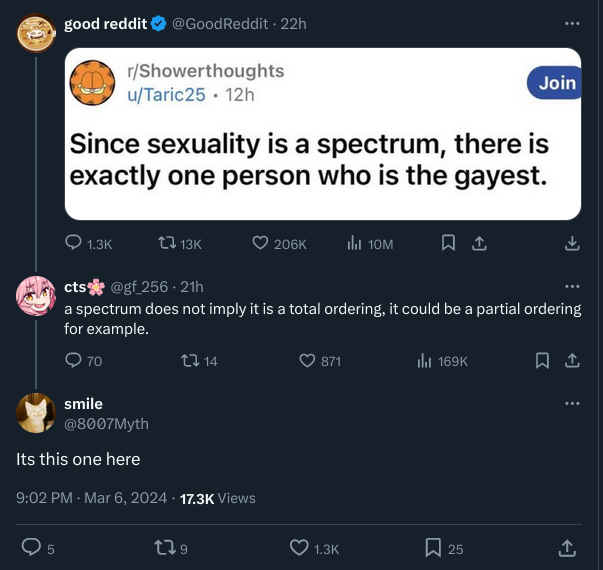
Well that's interesting: in order to define unmeasurable sets, you relied on the axiom of choice... I suppose it might be possible to define unmeasurable sets without AC, but maybe not!
Every time I encounter the axiom of choice implying a bunch of crazy stuff, it always loop back to requiring AC. It's like a bunch of evidence against AC!
I find it interesting that the basic description of AC sounds very plausible, but I'm still convinced mathematicians might have made the wrong choice... (See what i did there? ๐)
It's required, but nontrivially so. It has been proven that ZF + dependent choice is consistent with the assumption that all sets of reals are Lebesgue measurable.