this post was submitted on 27 May 2024
975 points (100.0% liked)
196
18536 readers
108 users here now
Be sure to follow the rule before you head out.
Rule: You must post before you leave.
Other rules
Behavior rules:
- No bigotry (transphobia, racism, etc…)
- No genocide denial
- No support for authoritarian behaviour (incl. Tankies)
- No namecalling
- Accounts from lemmygrad.ml, threads.net, or hexbear.net are held to higher standards
- Other things seen as cleary bad
Posting rules:
- No AI generated content (DALL-E etc…)
- No advertisements
- No gore / violence
- Mutual aid posts are not allowed
NSFW: NSFW content is permitted but it must be tagged and have content warnings. Anything that doesn't adhere to this will be removed. Content warnings should be added like: [penis], [explicit description of sex]. Non-sexualized breasts of any gender are not considered inappropriate and therefore do not need to be blurred/tagged.
If you have any questions, feel free to contact us on our matrix channel or email.
Other 196's:
founded 2 years ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
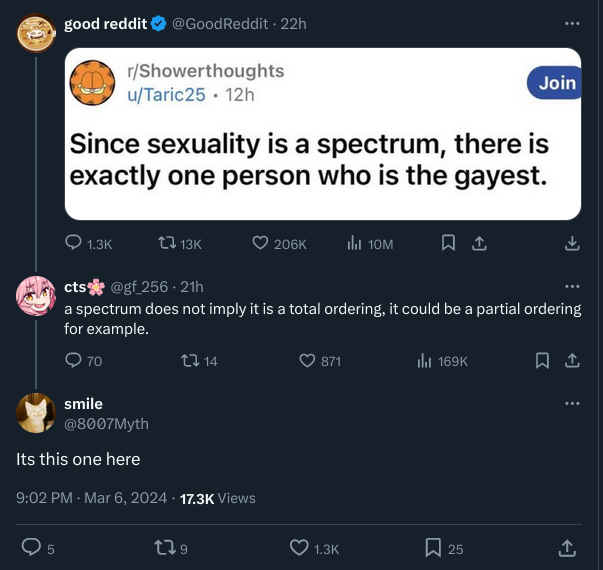
There are finitely many particles in the observable universe (that is to say, an infinite number will not fit), and a finite granularity to discern the position of those particles. That means there are finitely many configurations of particles within the volume of the observable universe.
Therefore, there are finitely many discernable things, so in a meaningful sense we can say with confidence that there's a finite variety of macroscopic things.
Whether or not an infinite number of particles will fit or not is not important, no ? I'm not sure what you mean by finite granularity. There is no "grid", space is continuous, the planck length and the fact that push on each other doesn't really factor in. By virtue of space being continuous and particles being finite, means you can configure stuff in infinite ways.
Edit: Not quoting you with the reference to a grid. I know that's not what you mean.
Are you aware of the plank length? It's the distance less than which which we can no longer determine if 2 things are any closer.
Don't worry, I understand.
Yes, but distance is still continuous, a minimum measurable distance (between stuff) doesn't make space granular. I suppose there might be a minimum measurably meaningful number of configurations, but I'm not super convinced.
My claim accounts for the possibility that the distances of particles may physically differ by amounts more granular than a plank length. My statement was that they are indiscernable. There are infinite copys of every person more closely identical than the two most similar identical twins. So closely identical that no physically possible device could ever distinguish between them. We cannot know if space is continuous. We simply know that if it is not continuous, it is of granularity as fine or finer than the plank length. So there is a meaningful sense in which there are finitely many macroscopic objects.