this post was submitted on 08 May 2024
635 points (97.2% liked)
Memes
45742 readers
1627 users here now
Rules:
- Be civil and nice.
- Try not to excessively repost, as a rule of thumb, wait at least 2 months to do it if you have to.
founded 5 years ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
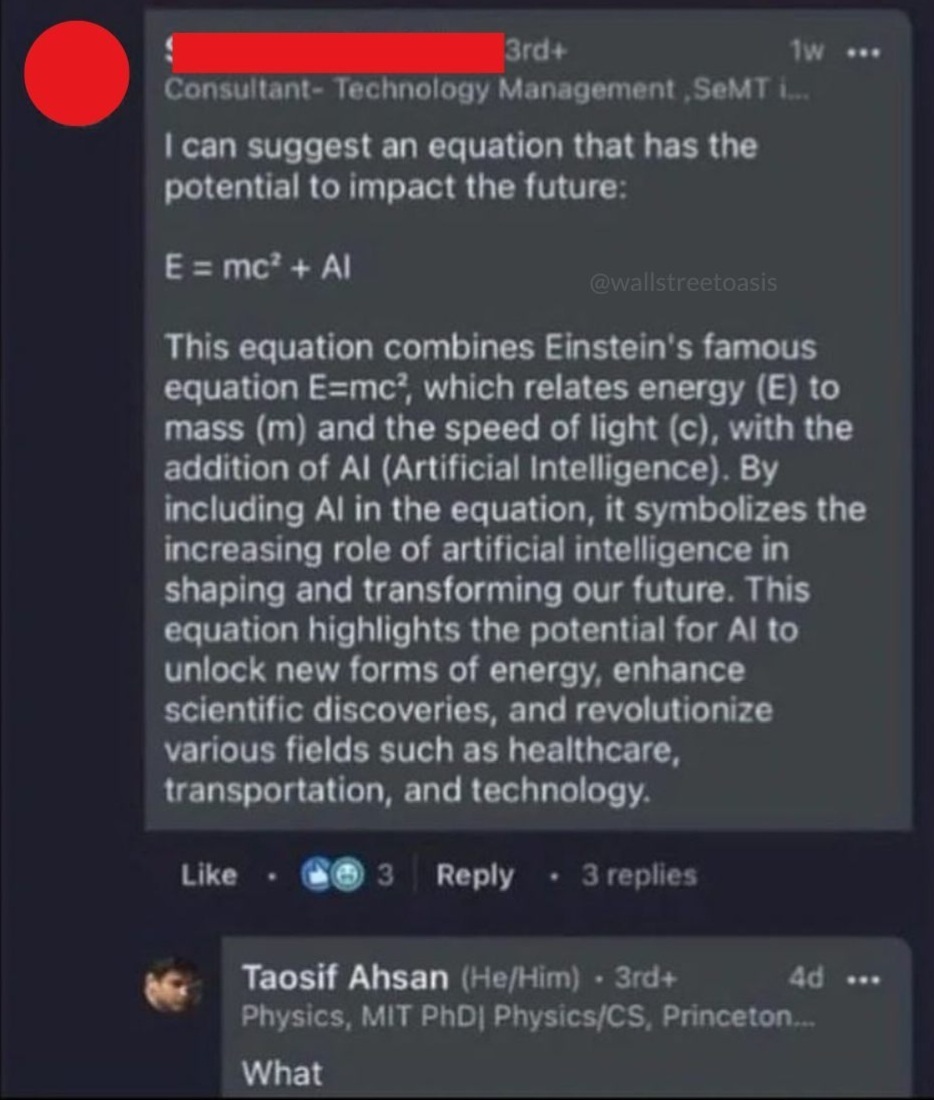
AI = 0 □
(MC^2 + C√P)^2 wouldn't give you that result though, because you have to FOIL.
Instead you'd get M^(2) C^4 + 2MC^(3)√P + PC^2
And that's not even the correct formula. It's
E^2 = (mc^(2))^2 + (pc)^2
You can't just naively apply a square root unless one of the terms is vanishing (momentum for a stationary mass, giving E = mc^2, or rest mass for a massless particle, giving E = pc = hf).
The way to remember this is that it's equivalent to the Pythagorean theorem, A^2 + B^2 = C^(2).
So it in fact only makes sense if AI = 0.
In my experience, when E=mc² is written, physicists generally mean relativistic mass, making the formula extract, whereas m_0 is used for rest mass, as seen in the expansion E = m_0c² + m_0v²/2 + O(v⁴)
Where does that expansion come from? As far as I can tell, m0v^(2)/2 only gives you the kinetic energy of the object where v << c, in which case the difference between relativistic mass and rest mass is negligible?
And where does the O(v^4) term come from?
This really seemed like a good simplification until you threw in that d'Alembert operator at the end