this post was submitted on 29 Sep 2023
1515 points (95.9% liked)
Memes
52901 readers
560 users here now
Rules:
- Be civil and nice.
- Try not to excessively repost, as a rule of thumb, wait at least 2 months to do it if you have to.
founded 6 years ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
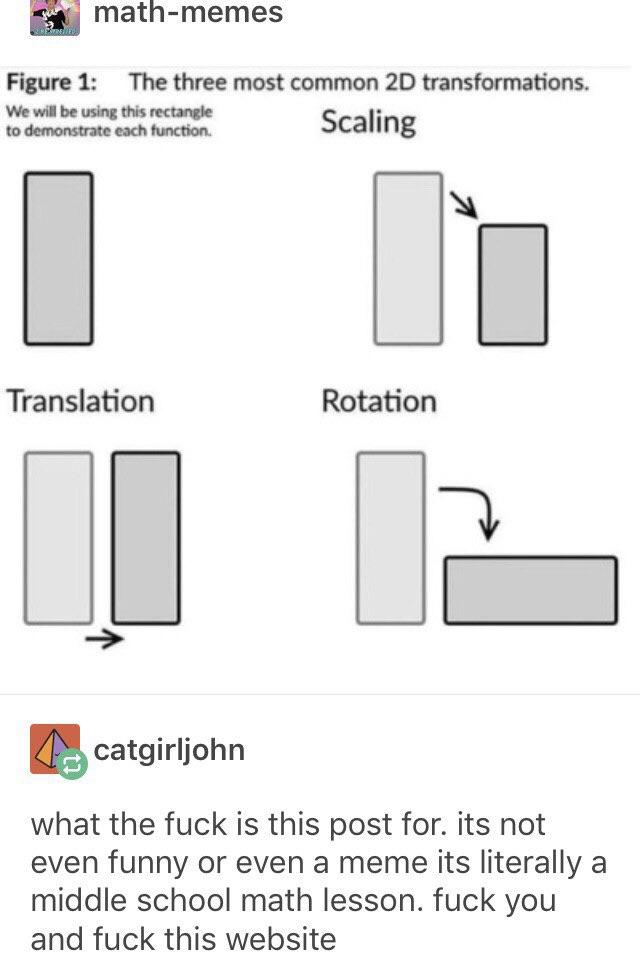
I'm irrationally agitated about Scale and Rotation involving a translation and that this is not called out in the meme.
Like it looks like "translation" is just "nothing happens" and this is going to bother me all day please help.
Translation just means all the coordinates of the points of the rectangle are moved the same increments. So the rectangle is the same length, width , and area, but the location of all of its vertices are different after translation. There's should be an x y plot to show this.
It's not entirely inaccurate in the case of rotation, since the composition of a rotation (with angle not a multiple of 2pi) and a translation is also a rotation with a new center.
R e a l l y?
I believe you, but what do I need to read to understand why that is?
There are many ways to prove it but my preferred one is by using complex numbers. In what follows we identify 2D points and vectors with their complex representation so that we won't have to deal with too many notations.
Let there be three points
z,z'andz'', and assume that:z'is obtained fromzby applying a rotation of angleθand centeru;z''is obtained fromz'by applying a translation byv.That means that we have:
z' - u = (z - u) * exp(i * θ)z'' = z' + vIn particular, we have:
z'' = u + v + (z - u) * exp(i * θ)It kinda looks like a rotation is there, since we have a
exp(i * θ), so we'd ideally like to have the right-hand side in the above equality be in the formw + (z - w) * exp(i * θ).Let's see if we can achieve that, we'll look for
wsuch that:w + (z - w) * exp(i * θ) = u + v + (z - u) * exp(i * θ)Which after some simplifications becomes:
w * (1 - exp(i * θ)) = u * (1 - exp(i * θ)) + vAnd assuming that
θis not a multiple of2 * pi, we can divide both sides by1 - exp(i * θ)and we get:w = u + v / (1 - exp(i * θ))(from here you can easily further simplify to get the explicit 2D coordinates ofw)So what we've shown is that there indeed exists a unique center
wsuch thatz''is obtained fromzby applying a rotation of angleθaroundw, ie:z'' - w = (z - w) * exp(i * θ)And scale only scales one dimension… the width is unchanged.
The rotation one still works. It's just being rotated around a very specific point to get there.
I think I know what you mean, but is there any point you can rotate around to get that transformation without a translation? Where would that point need to be?
Here's the video where I actually learned about this phenomenon!
https://youtu.be/1EpQtVJb0OU?si=arWTbgH0UiB_9cgP
Oh wow that video is actually really good. I was hoping there would be 100 more like it on that channel, but it looks like kind of a one off.
Yeah, I went ahead and subscribed anyways. It's the first time he's done a video like that, but it was by far his most successful video. Hopefully there are more to come
Here is an alternative Piped link(s):
https://youtu.be/1EpQtVJb0OU?si=arWTbgH0UiB_9cgP
Piped is a privacy-respecting open-source alternative frontend to YouTube.
I'm open-source; check me out at GitHub.